Rectas paralelas cortadas por una recta secante

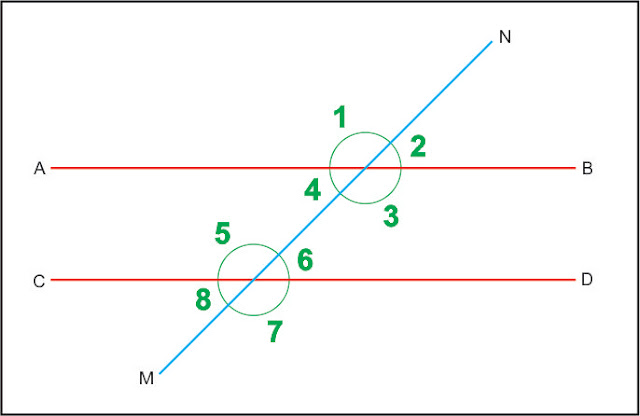
Si las rectas paralelas, AB y CD son cortadas por una recta secante MN, se forman los siguientes ángulos:

Ángulos alternos internos: Ángulos internos no adyacentes situados en distinto lado de la secante; son iguales.

∠3=∠5;    ∠4=∠6 

 Ángulos alternos externos: Ángulos externos no adyacentes situados en distinto lado de la secante; son iguales.

∠1=∠7;    ∠2=∠8 

 Ángulos correspondientes: Dos ángulos no adyacentes situados en un mismo lado de la secante; son iguales.

∠ 1 = ∠ 5;    ∠ 4 = ∠ 8;    ∠ 2 = ∠ 6;    ∠ 3 = ∠ 7

Ángulos colaterales internos (suplementarios): Dos ángulos internos no adyacentes y situados del mismo lado de la secante; suman 180°.

∠ 4 + ∠ 5 = 180°;     ∠ 3 + ∠ 6 = 180°

Ángulos colaterales externos (suplementarios): Ángulos externos no adyacentes situados del mismo lado de la secante; suman 180°.

∠ 1 + ∠ 8 = 180°;     ∠ 2 + ∠ 7 = 180°

Ángulos opuestos por el vértice: Son aquellos que tienen el vértice común, y los lados de uno de los ángulos son la prolongación de los del otro.

Los ángulos opuestos por el vértice son iguales:

Ángulos contiguos: Son aquellos que tienen un lado y un vértice en común.

∠ AOB es contiguo a ∠ BOC, entonces:

Ángulos adyacentes: Son ángulos contiguos cuyos ángulos no comunes están alineados, esto es, suman 180⁰.

∠ AOB es adyacente a ∠ BOC, entonces: